Materials and Methods

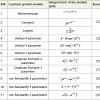
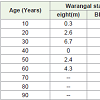
The integral forms of Monomolecular, Gompertz, Logistic, Weibull (two, three and four parameters), Von Bertalanffy (two, three and four parameters) and Chapmen Richard (three and four parameter) growth models are shown in Table 1. The data composed in the Table 2 are of height and DBH growth data from Teak trees in Warangal state and Hoshangabad division of India [1].

Table 1: The integral forms of the growth models along with the source.

Table 2: Height and DBH growth data from Teak trees in Warangal state and Hoshangabad division of India.

Here A,B,K,d,β,b₁,b and m are parameters to be estimated, y is the dependent growth variable, t is the independent variable and exp(e) is the base of the natural logarithms. The parameters of the growth models are defined as: A is the asymptote; K is the parameter governing the rate at which the regress and approaches its potential maximum; m is the allometric constant; d is the instant rate of growth in the inflection point, b is the value of the growth at the initial age and B, β and b1 are biological constants.

The different growth models can be written in the form as

i=1,2,....,n, where B is the vector of parameters b_j (b₁,b₂...,b_s) to be estimated, s is the number of parameter, n is the number of observations and ε_i’s are random errors in the models has mean zero and constant variance σ². The following methods of estimation have been used to fit the growth models.

Method of Estimation

The parameters of Monomolecular, Logistic and Gompertz growth have been estimated using the technique used by Borah and Mahanta [2]. The generalized Newton Raphson technique used in Mahanta and Borah are applied to estimate the parameters of Weibull growth models [3]. The new methods for the estimation of the parameters of Von Bertalanffy and Chapmen Richard growth models are described as follows.

Methods to estimate the parameters of Chapmen Richards’sgrowth model

Fitting of the four parameters model

Method I: In this method, first assume that the parameter d is known from its definition. Assume n be the total number ofobservation and let t_a,t_b and t_c are any three observations from the set of data. Then for i = a,b,c the Chapmen Richards growth model with four parameters can be written as

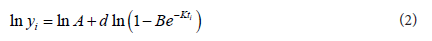
Now,

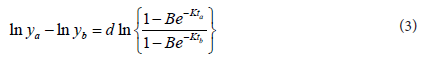
and

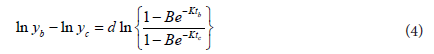
From the equation (3) and (4),

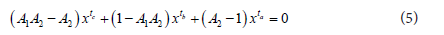
Where

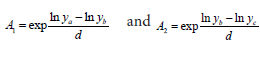
The equation (5) can be solved using any iteration method, and then the parameter K can be estimated as,

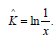
After estimation of the parameter K; the parameters B, A and d can be estimated using the equations (2), (3) and (4). The required estimated parameters are given by

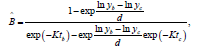
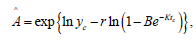
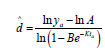
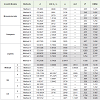
Table 3: Estimation of parameters along with the summary of statistical analysis to height growth data from Hoshangabad division.

Figure 1: Observed data along with the top two results for height growth data of Hoshangabad.

Table 4: Estimation of parameters along with the summary of statistical analysis to DBH growth data from Hoshangabad division.

Table 5: Estimation of parameters along with the summary of statistical analysis to height growth data from Warangal state.

Table 6: Estimation of parameters along with the summary of statistical analysis to DBH growth data from Warangal state.

Table 7: 95% Confidence intervals of the parameters of surviving growth models.

Figure 2:Observed data along with the top two results for DBH growth data of Hoshangabad.

Figure 3:Observed data along with the top two results for height growth data of Warangal.

Figure 4:Observed data along with the top two results for DBH growth data of Warangal.